使用 shonDy 进行齿轮箱润滑仿真

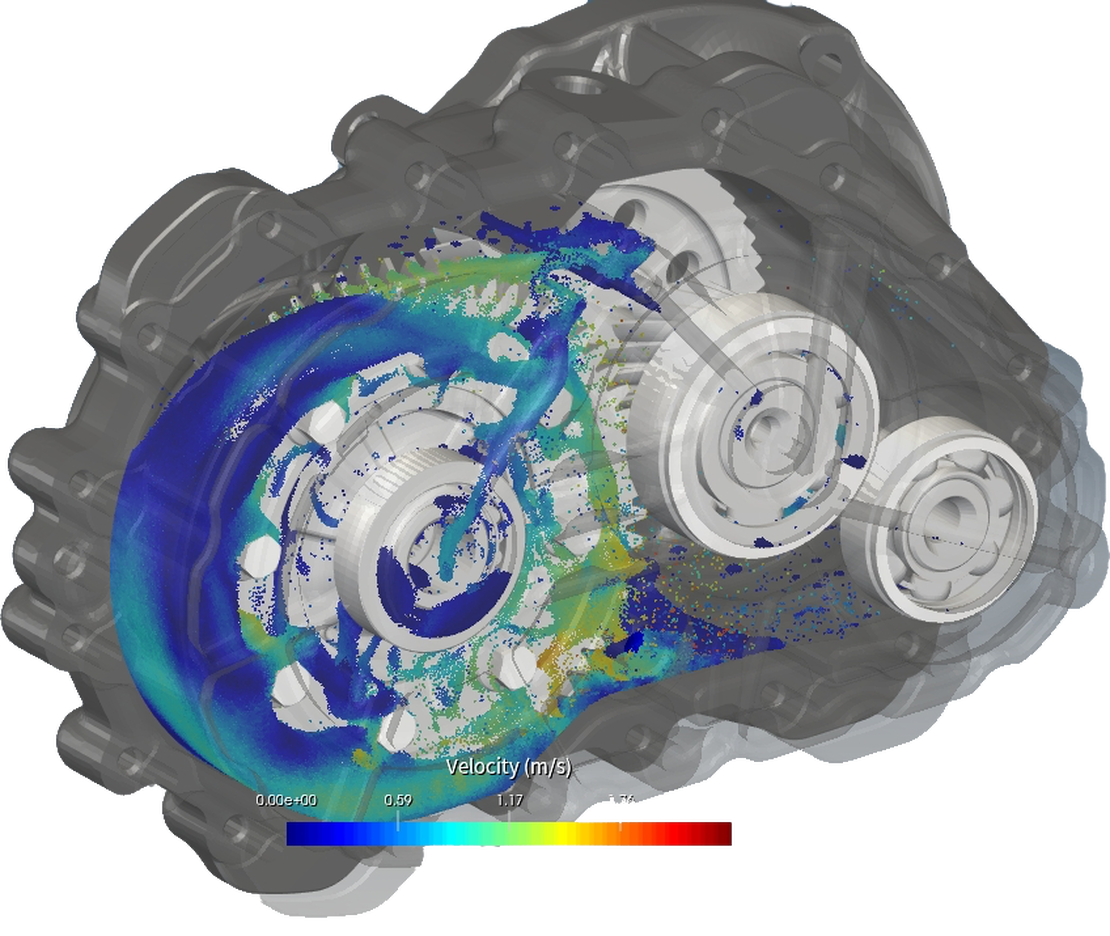
齿轮润滑是维持高效耐用的齿轮系统的关键方面。它涉及使用润滑剂来减少摩擦、散热并防止齿轮机构的磨损和腐蚀。适当的齿轮润滑可确保平稳运行，延长零部件的使用寿命，并有助于提高整个系统的可靠性。

如需了解通用方法而非本案例的具体内容，请参阅我们的博客文章 齿轮箱润滑：仿真与实验对比，文中介绍了飞溅润滑难以仿真的原因以及基于粒子的 CFD 如何应对这一挑战。

案例描述

在此案例中，目的是将模拟结果与实验结果进行比较。在润滑方面，下图中标记的区域对于润滑至关重要。红色圆圈突出显示轴承，箭头表示通向轴承前面这些腔室的小通道。在模拟中，这些区域通过采样窗口进行监测，以定量了解轴承内的液体量和腔内的流量。在实验的图片中，相同的区域以绿色突出显示。为了有效地润滑轴承，必须通过通道将润滑剂注入腔内。通过将不同旋转速度下的这些关键区域与实验结果进行比较，可以确定模拟的准确性。

案例设置

为了进行模拟，使用了与实验中相同量的润滑剂，即 300 毫升。选定的粒子半径为 0.42 毫米，因此粒子数量约为 50 万个。下表显示了该液体的性质。根据这些性质，该流体在 20°C 时可作为润滑剂。

这里使用的变速箱采用正齿轮。该变速箱内有两个具有不同传动比的齿轮组。第一对齿轮的传动比为 0.4468。第二对齿轮的传动比为 0.3607。这些比率组合在一起可产生 0.1611 的总传动比，从而导致输入轴每转一圈，输出轴的转速为 0.1611 转/分钟（RPM）——从变速箱的输入到输出的速度大幅降低。

受检案例：

仿真结果

案例1：480 RPM

在下面提供的视频中，我们观察案例1，其中输入速度设置为480 RPM。

分析模拟结果可以发现，77 RPM 的输出速度不足以充分填充位于变速箱顶部的小水池。视频中，水池用红色圆圈标记。动态结果表明，大齿轮与液体啮合，将其提升至齿轮高度的约三分之二，然后落回储液器。

因此，通向中腔的通道无法以这种速度被填满。此外，通往左侧腔室的通道未与水池相连，也仍处于未充满状态。

可以得出结论，在此输出速度下，轴承没有润滑。输出速度阻碍了流体正常流向重要部件。

将模拟结果与实验视频进行比较，可以说模拟结果与实验结果高度一致。

案例2：980 RPM

在下面的视频中，案例 2 的输入速度为 980 RPM。

根据仿真结果，158 RPM 的输出速度足以填满顶部的小池子。因此，通向中间腔室的通道充分充满液体。此外，通往左腔室的通道也被填满。值得注意的是，水池和左腔室都没有充满连续的润滑剂流，而是充满振荡流。

在指定输出速度下，水池和左腔室的成功填充表明与案例 1 相比性能有所改善，展示了输入速度在实现中腔室和左腔室的适当润滑和流体分布方面的重要性。不幸的是，右腔室没有通过连接中间腔室和左腔室的通道填充。

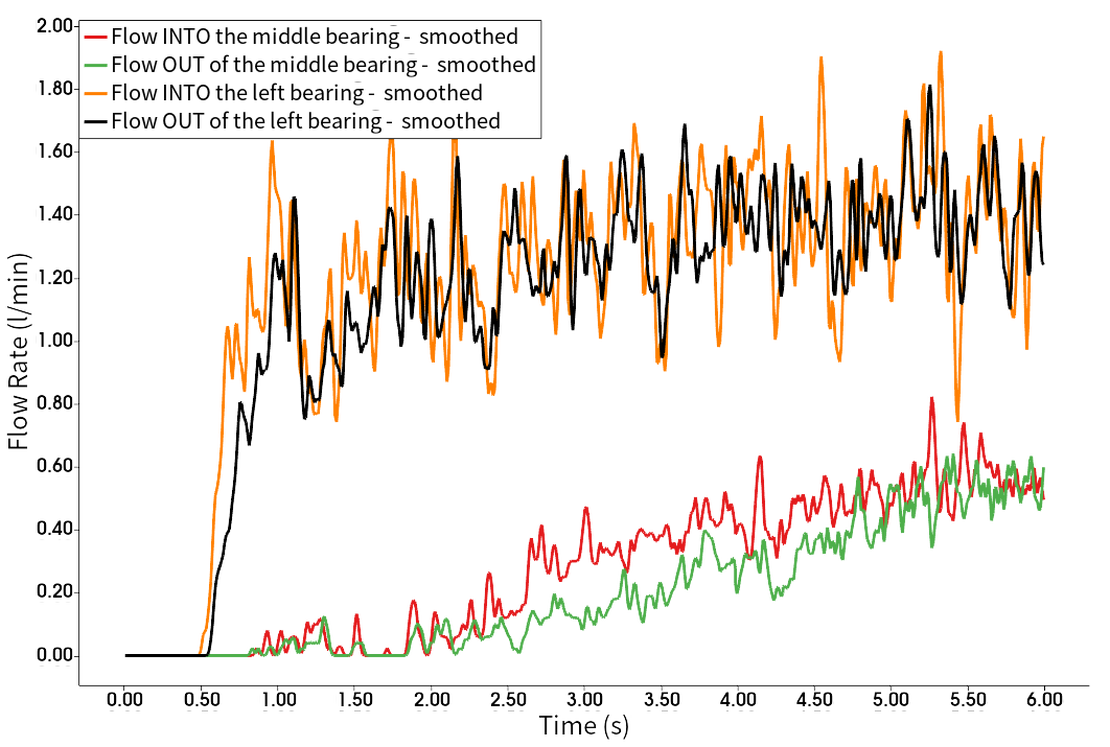
为了将仿真结果与实验结果进行比较，必须达到准稳态。这种状态的一个指标是样品窗口的平衡，表示平均而言，流入和流出样品窗口的液体流量几乎相同。下图说明了这些感兴趣的流。

在左侧轴承中，大约 2 秒后就已经达到稳定状态，而中间轴承则需要更长的时间。5 秒后，可以断言中间轴承已达到稳态。该分析强调了在仿真和实验结果之间进行有意义的比较之前，留出足够的时间让系统稳定的重要性。

将模拟的这些观察结果与实验视频进行比较，可以注意到，从视觉上看，左腔室与实验结果非常吻合。然而，在变速箱的顶部明显存在轻微的过度预测行为。模拟表明水池的填充不可忽略，但在仔细检查实验视频的第二部分（从 6 秒开始）后，很明显，尽管液体似乎接触到水池的底部，但大部分液体没有进入水池。因此，与模拟相比，通往中间腔室的通道输送的流体似乎更少。

案例3：1453 RPM

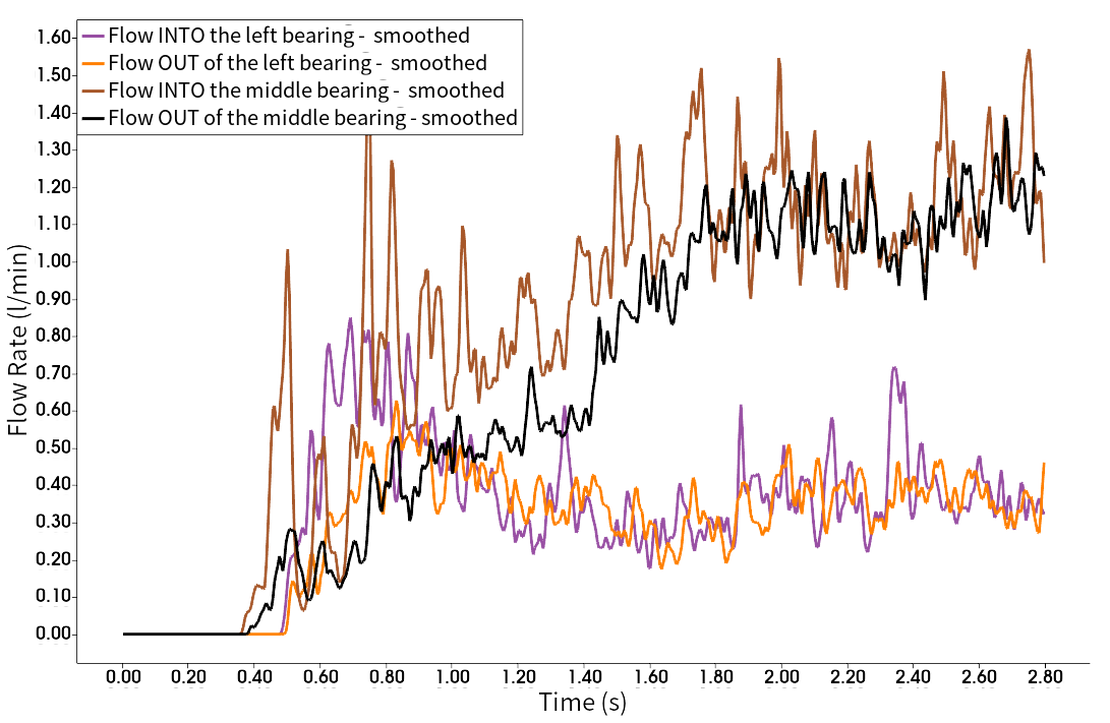
尽管案例 3 的输入速度高于案例 2，但润滑过程的整体性能几乎相同。与案例 2 类似，左侧和中间轴承的腔室已充分填充，而右侧轴承和腔室的润滑剂很少甚至没有。与案例 2 的主要区别在于，在案例 3 中更早达到稳态。这可以在下图中观察到，说明了进出左侧和中间轴承采样窗口的流量。

在两个轴承中，都达到平衡，表明流入样品窗口的流体量与流出的流体量相同。根据图，1.8 秒后已经达到稳定状态。这种早期达到的稳态表明，与案例 2 相比，案例 3 中的润滑过程稳定得更快。然而，右轴承和腔室润滑不足的持续问题仍然存在，需要进一步调查或修改以应对这一特定挑战。

将模拟的这些观察结果与实验视频进行比较，可以注意到，从视觉上看，左腔室略微低估了实验视频中的填充。另一方面，在模拟和实验中，水池的填充看起来相当。因此，在模拟和实验中，通往中间腔室的通道比案例 2 输送的流体更多。

结论

在案例 1（480 RPM）中，模拟结果与实验结果高度一致，揭示了在指定输出速度下润滑不足的问题。案例 2（980 RPM）证明了润滑性能的提高，模拟和实验之间具有良好的一致性。在案例 3（1453 RPM）中，模拟捕捉到了早期稳定状态和一致的趋势，与实验观测结果的一致性令人满意，尤其是在齿轮箱顶部水池注水时。

分辨率研究

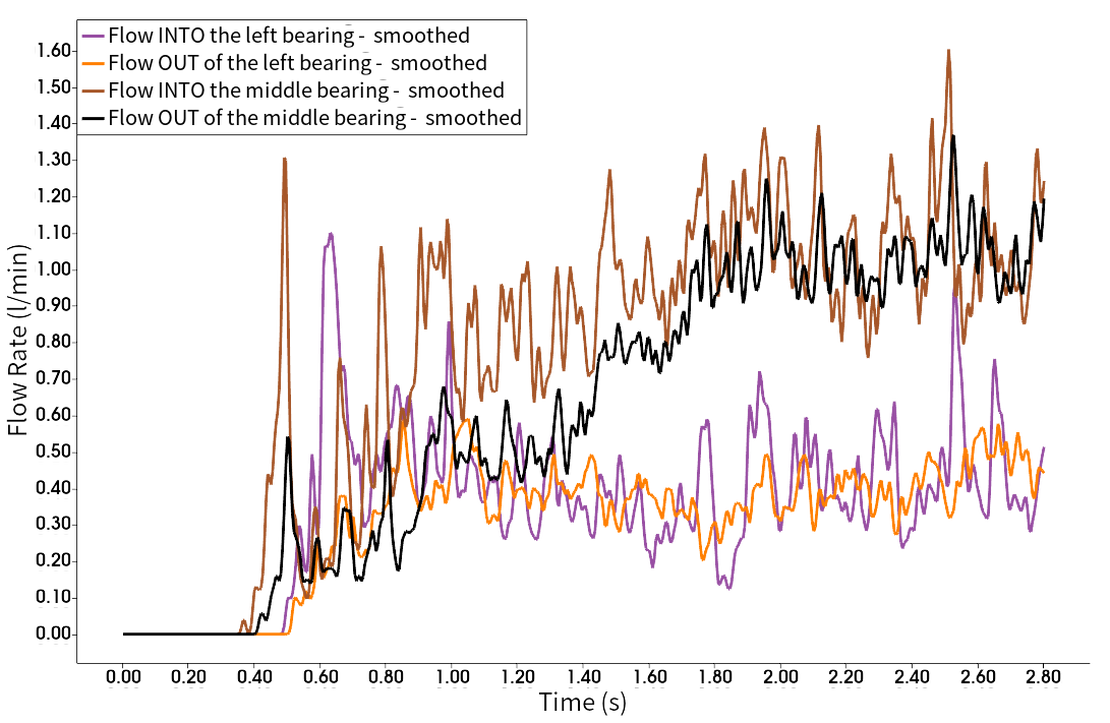
在传统的有限体积法（FVM）CFD 模拟中，网格研究很常见，而在基于粒子的方法中，对应的是粒子尺寸研究。在此模拟中，最初进行了粒子尺寸研究，并在最后部分予以介绍，展示了两种分辨率：基本情况（案例 3）有 50 万个粒子，更高分辨率的情况（案例 3 高分辨率）有 100 万个粒子。以进出轴承的流量作为参考值，两种情况表现出相当的行为，如下图所示，证实了 50 万个粒子对于这些场景已经足够。两次模拟的 2.4 秒快照进一步支持了这一点，表明了相似的液体分布和行为。

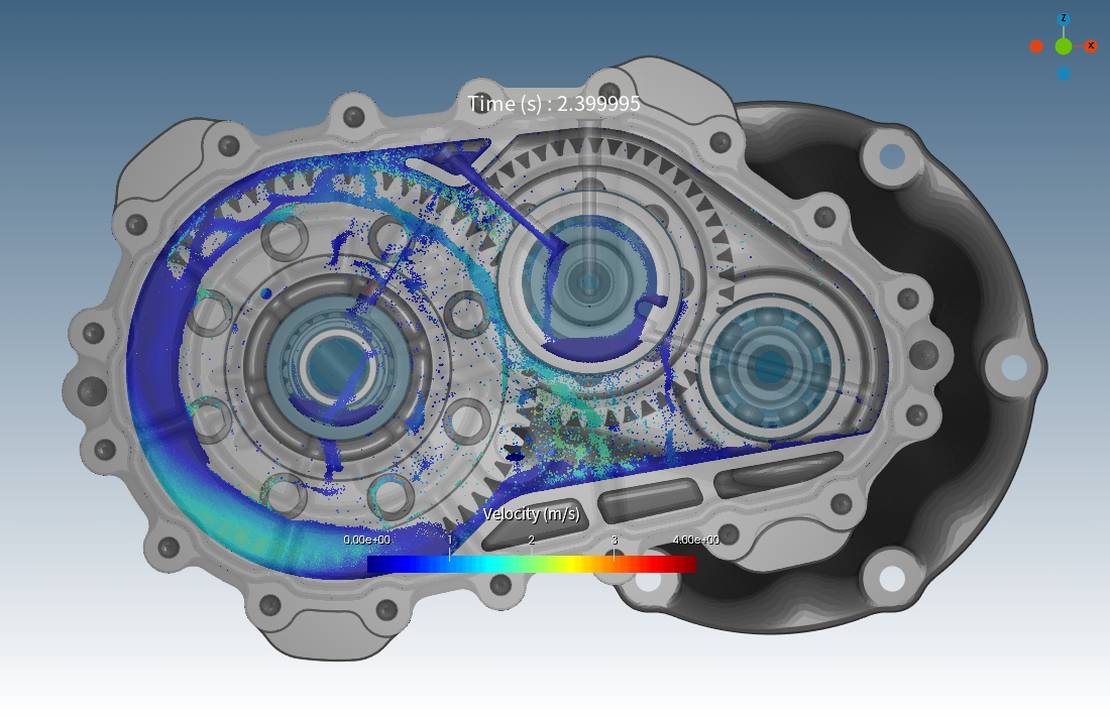
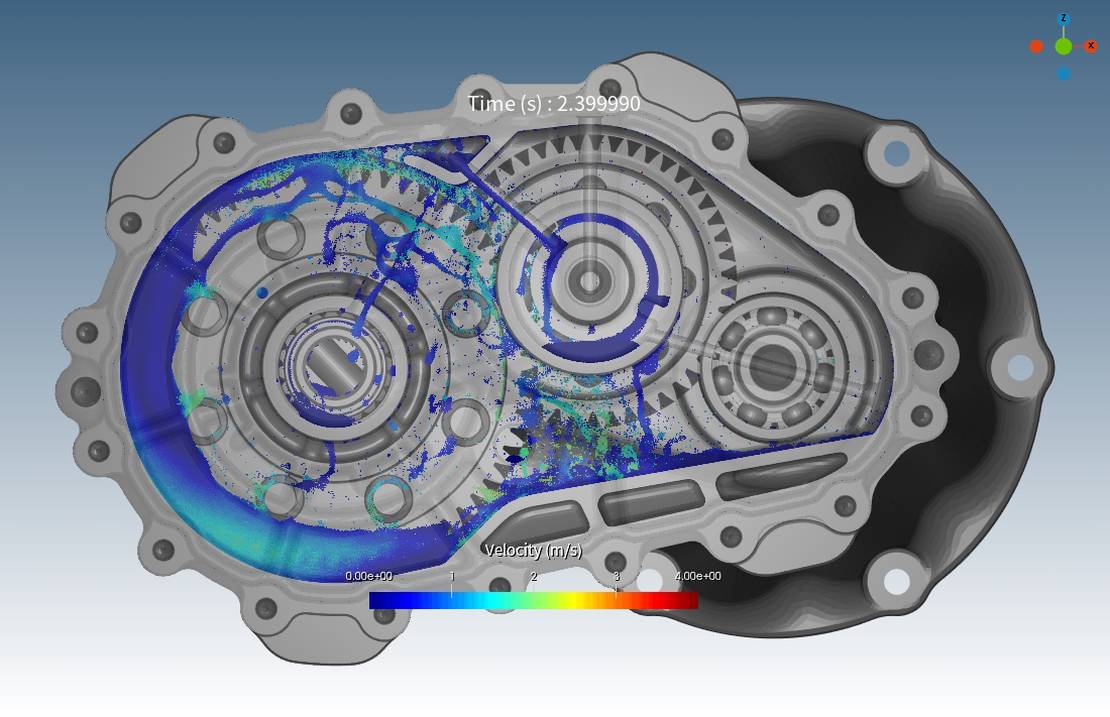
计算统计概要

模拟使用 2.6 版进行

预计版本 2.7 将显著提升运行速度。如需直接对比版本 2.6 和 2.7 的性能，请参考 车辆涉水案例。