Verständnis der Lumped-Parameter Thermal Network (LPTN) Methode (1/2)

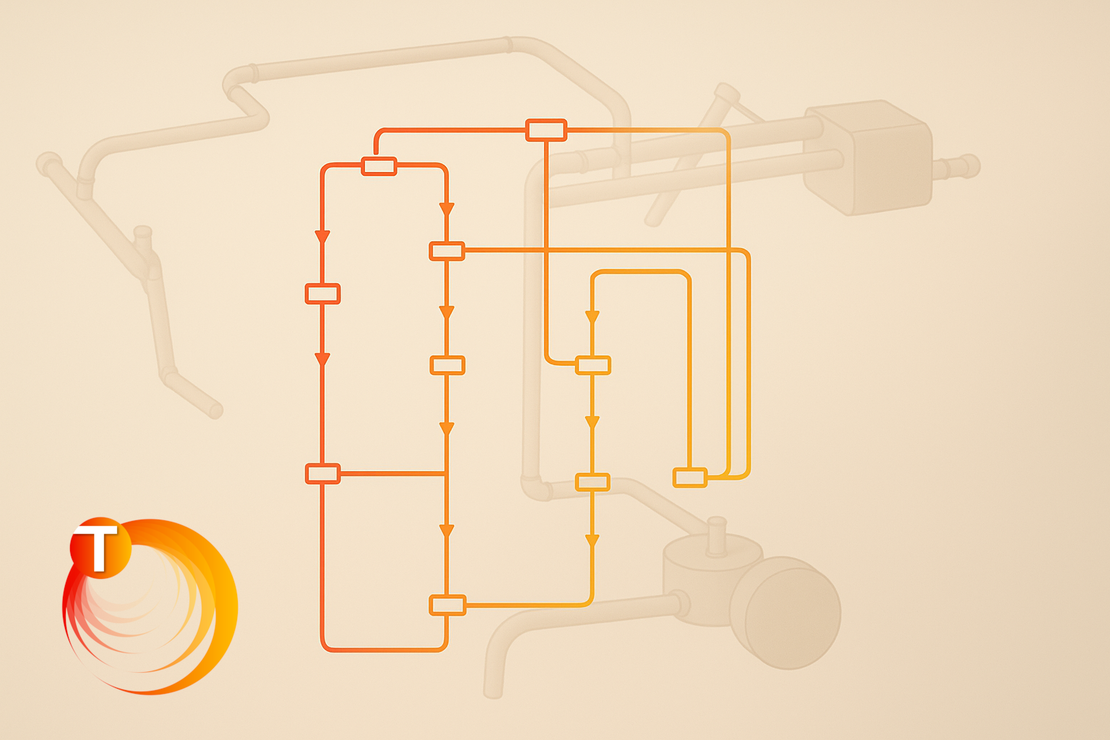
Bei der Produktentwicklung ist es von entscheidender Bedeutung, das Gesamttemperaturprofil des Produkts und den Energietransfer zwischen seinen Komponenten zu verstehen, anstatt sich ausschließlich auf die Temperaturverteilung innerhalb einzelner Komponenten zu konzentrieren. Um dies zu bewältigen, besteht Bedarf an einer Simulationsmethode, die Berechnungen effizient vereinfachen und beschleunigen kann, während ein akzeptables Maß an Genauigkeit beibehalten wird. Die Lumped-Parameter Thermal Network (LPTN) Methode erfüllt diese Kriterien effektiv. Das Prinzip hinter dieser Methode wird in Abbildung 1 dargestellt.

Wie in Abbildung 1 gezeigt, werden die physikalischen Eigenschaften eines Systems innerhalb eines Kontrollvolumens an den Knoten (a, b, c, d und e) aggregiert. Die Temperatur an diesen Knoten ist eine Darstellung der Gesamttemperatur des Systems. Diese Knoten sind durch Wärmeübertragungspfade miteinander verbunden und bilden ein komplexes thermisches Netzwerk. Entlang jedes Pfades wirkt der thermische Widerstand, analog zum elektrischen Widerstand, als Widerstand gegen den Energietransferprozess. Die Vereinfachung und Modellierung des Systems ist mit der thermischen Netzwerkmethode möglich.

Knoten und thermischer Widerstand sind die Grundkomponenten der LPTN-Methode. Diese Methode hängt weiterhin von der Art der Wärmeübertragung und anderen physikalischen Szenarien ab.

Klassifizierung der Knoten

In LPTN repräsentieren Knoten die physikalischen Eigenschaften des Systems innerhalb eines Kontrollvolumens, einschließlich Volumen, Masse, Materialeigenschaften und Temperatur. Knoten können abhängig von ihrer Wärmekapazität in drei Typen klassifiziert werden, und zwar:

• Oberflächenknoten: Repräsentieren eine Oberfläche mit null Volumen und folglich null Wärmekapazität.
• Volumenknoten: Repräsentieren die Masse eines Kontrollvolumens und aggregieren dessen physikalische Eigenschaften (Masse, Volumen, Materialeigenschaften). Sie besitzen endliche Wärmekapazität und speichern thermische Energie.
• Randknoten: Repräsentieren eine Umgebung oder Wärmequelle mit fester Temperatur. Da ihre Temperatur unabhängig vom Wärmeaustausch konstant bleibt, werden sie als mit unendlicher Wärmekapazität betrachtet.

Thermischer Widerstand

Der thermische Widerstand hängt von der Art des Energietransfers ab. Die Art der Wärmeübertragung kann in vier Typen kategorisiert werden:

1. Wärmeleitung
2. Konvektion
3. Strahlung
4. Stoffübertragung (Sonderfall)

Die ersten drei Arten der Wärmeübertragung, Leitung, Konvektion und Strahlung, unterliegen dem Grundprinzip des Energieflusses von Bereichen höherer Temperatur zu Bereichen niedrigerer Temperatur, angetrieben durch Temperaturgradienten. Die vierte Art ist einzigartig und beruht auf Massentransport anstatt auf Temperaturgradienten. Berechnungen des thermischen Widerstands werden im nächsten Abschnitt detailliert beschrieben.

Erhaltungsgleichungen und Berechnung des thermischen Widerstands

Erhaltungsgleichungen

Für jeden diskreten Knoten in Abbildung 1 gilt das Prinzip der Energieerhaltung:

$$\sum_{j=1}^{n} \dot{Q}_{ij} + S_i = \rho_i V_i C_{pi} \frac{dT_i}{dt} \tag{1}$$

wobei Qij den Wärmefluss zwischen Knoten i und Knoten j in Watt [W] darstellt; d.h. den Energietransfer zwischen den Knoten i und j. Es ist zu beachten, dass die in Knoten i einfließende Energie negativ ist und die aus Knoten i ausfließende Energie positiv ist. Hier ist Si die Wärmequelle für Knoten i in W; ri, Vi, Cpi und Ti sind die Dichte in kg/m3, das Volumen in m3, die spezifische Wärmekapazität in J/kg.K und die Temperatur des Knotens i in K.

Die Bedeutung von Gleichung (1) ist, dass die in Knoten i einfließende Nettoenergie gleich der in Knoten i gespeicherten Energie ist. Für ein stationäres Problem, bei dem sich die Temperatur nicht mit der Zeit ändert, ist die rechte Seite der Gleichung null.

Der Ausdruck für den Wärmefluss zwischen den Knoten i und j ist (analog zu Strom = Spannungsdifferenz/Widerstand):

$$\dot{Q}_{ij} = \frac{T_i - T_j}{R_{ij}} \tag{2}$$

wobei Rij der thermische Widerstand zwischen den Knoten i und j ist und den Widerstand gegen den Energietransfer darstellt.

Berechnung des thermischen Widerstands

Umformulierung von Gleichung (2) ergibt:

$$ R{ij} = \frac{T_i - T_j}{\dot{Q}{ij}} \tag{3}$$

Daher müssen wir die Beziehung zwischen Qij und der Temperaturdifferenz an Knoten i finden, um den Ausdruck für den thermischen Widerstand zu erhalten.

Wärmeleitung:

Gemäß dem Fourier-Gesetz:

$$\dot{Q}_{ij} = k \cdot \frac{T_i - T_j}{l} \cdot A \tag{4}$$

Wobei l die charakteristische Länge in m, k die Wärmeleitfähigkeit in W/mK und A die Wärmeübertragungsfläche in m2 ist. Das Einsetzen von Gleichung (4) in Gleichung (3) ergibt:

$$R_{ij} = (T_i - T_{ref}) \cdot \frac{1}{hA(T_i - T_{ref})} = \frac{1}{hA} \tag{5}$$

Thermische Konvektion:

Gemäß Newtons Abkühlungsgesetz:

$$\dot{Q}_{ij} = h \cdot (T_i - T_{ref}) \cdot A \tag{6}$$

wobei h der konvektive Wärmeübertragungskoeffizient in W/m2K, Tref die Referenztemperatur in K und A die Wärmeübertragungsfläche in m2 ist. Analog ergibt das Einsetzen von Gleichung (6) in Gleichung (3):

$$R_{ij} = (T_i - T_{ref}) \cdot \frac{1}{hA(T_i - T_{ref})} = \frac{1}{hA} \tag{7}$$

Wärmestrahlung:

Unter der Annahme, dass die Strahlung von Knoten i zu Knoten j zu einem schwarzen Körper erfolgt, d.h. der Sichtfaktor 1 ist (d.h. die gesamte von Knoten i emittierte Energie wird von Knoten j absorbiert), erhalten wir:

$$\dot{Q}_{ij} = \epsilon \sigma(T_i^4 - T_j^4)A = \epsilon \sigma(T_i^3 + T_i^2T_j + T_iT_j^2 + T_j^3)(T_i - T_j)A \tag{8}$$

wobei ε die Boltzmann-Konstante in W/m2K4, σ das Emissionsvermögen und A die Wärmeübertragungsfläche in m2 ist. Analog ergibt das Einsetzen von Gleichung (8) in Gleichung (3):

$$R_{ij} = (T_i - T_j) \cdot \frac{1}{\epsilon \sigma(T_i^3 + T_i^2T_j + T_iT_j^2 + T_j^3)(T_i - T_j)A} = \frac{1}{\epsilon \sigma(T_i^3 + T_i^2T_j + T_iT_j^2 + T_j^3)} \tag{9}$$

Gleichung (8) ist in Bezug auf die Temperatur nichtlinear. Um die Temperaturdifferenz (Ti−Tj) zu bewerten, muss die Gleichung linearisiert werden. Folglich ist der thermische Widerstand aufgrund von Strahlung vom Knoten abhängig, was iterative Berechnungen zur Lösung der Nichtlinearität erforderlich macht.

Stoffübertragung und Wärmeübertragung:

Betrachten Sie ein Rohr mit einer Flüssigkeit, die bei bekannten Ein- und Austrittstemperaturen Ti bzw. Tj strömt. Die Rate des Wärmeaustauschs, während die Flüssigkeit durch das Rohr fließt, beträgt:

$$\dot{Q}_{ij} = m \cdot \dot{C}_{pi} \cdot (T_i - T_j) \tag{10}$$

wobei ṁ der Massenstrom des Rohrs in kg/s und Cpi die spezifische Wärmekapazität der Flüssigkeit am stromaufwärtigen Knoten in J/kgK ist. Analog ergibt das Einsetzen von Gleichung (10) in Gleichung (3):

$$R_{ij} = (T_i - T_j) \cdot \frac{1}{m\dot{C}_p(T_i - T_j)} = \frac{1}{m\dot{C}_{pi}} \tag{11}$$

Die Gleichung des thermischen Widerstands variiert unter verschiedenen Szenarien. Faktoren wie die Wahl des Koordinatensystems (z.B. Umfangs-, Axial- und Radialrichtungen in Zylinderkoordinaten), temperaturabhängige Materialeigenschaften und Strahlungsaustausch unter Schwarzkörperannahmen führen zu unterschiedlichen Ausdrücken für den thermischen Widerstand. Daher ist es bei der Anwendung des thermischen Widerstands unerlässlich sicherzustellen, dass die Formel mit dem entsprechenden physikalischen Kontext übereinstimmt.

Berechnungsbeispiel

Das folgende eindimensionale Wärmeübertragungsbeispiel veranschaulicht den Berechnungsprozess unter Verwendung der LPTN-Methode.

Dieses Beispiel ist ein eindimensionales Wärmeleitungsproblem. Die Abmessungen des Festkörperblocks werden in Abbildung 2 dargestellt. Die Wärmeleitfähigkeit des Festkörperblocks beträgt k = 40W/mK, und T1=T2=293,15K sind die Randtemperaturen am linken und rechten Ende des Festkörperblocks.

Der erste Schritt bei der Anwendung der thermischen Netzwerkmethode besteht darin, die Geometrie in Knoten zu diskretisieren. Ein einzelner Volumenknoten repräsentiert den gesamten Festkörperblock, während Randknoten die Randbedingungen an beiden Enden repräsentieren. Dies ergibt einen Volumenknoten (Knoten 1) und zwei Randknoten (Knoten 2 und Knoten 3). Die Verbindung dieser drei Knoten entlang des Wärmeübertragungspfades ergibt das thermische Netzwerkdiagramm wie in Abbildung 2 gezeigt. Im Diagramm stellt PLoss die Wärmesenke aus dem Block dar. In diesem Fall gibt es keine Wärmequelle.

Basierend auf der Formel in Abschnitt 3 erhalten wir:

Der Wärmefluss zwischen Knoten m und Randknoten 1 beträgt:

$$\dot{Q}_{m1} = (T_m - T_1)/R_{th1} \tag{12}$$

Analog ist der Wärmeaustausch zwischen Knoten m und Randknoten 2:

$$\dot{Q}_{m2} = \frac{(T_m - T_2)}{R_{th2}} \tag{13}$$

wobei Rth1, Rth2 der thermische Widerstand ist. Da Symmetrie gilt, gemäß Abschnitt (5):

$$R_{th1} = R_{th2} = \frac{0.5l}{kab} = \frac{0.5 \cdot 0.1}{40 \cdot 0.03 \cdot 0.02} \approx 2.083\text{k/W} \tag{14}$$

Basierend auf Formel (1), für Knoten:

$$\dot{Q}_{m1} + \dot{Q}_{m2} - \frac{T_m - T_1}{R_{th1}} - \frac{T_m - T_2}{R_{th2}} = 0 \tag{15}$$

Das Einsetzen der Gleichungen (12) bis (14) in Gleichung (15) ergibt:

$$ \frac{T_m - T_1}{R_{th1}} + \frac{T_m - T_2}{R_{th2}} = 0 $$

$$T_m = \frac{T_1 R_{th2} + T_2 R_{th2}}{R_{th1} + R_{th2}} = \frac{293.15 \cdot 2.083 + 293.15 \cdot 2.083}{2.083 + 2.083} = 293.15\text{ K} \tag{16}$$

Ohne interne Wärmequellen und identischen Temperaturen an beiden Grenzen beträgt die theoretische Temperatur des gesamten Festkörperblocks ebenfalls 293,15K, was dem Ergebnis der LPTN-Methode entspricht.

Um den Festkörperblock mit n Knoten zu diskretisieren, kann für jeden gegebenen Knoten i eine Energieerhaltungsgleichung (d.h. Gleichung (1)) formuliert werden. Mit n Knoten ergeben sich n lineare Gleichungen, die als Matrix aij Tj = bi (Ax=b) geschrieben werden können. Mithilfe eines linearen Algebra-Lösers können die Temperaturen an jedem Knoten gelöst werden.

Wenn diesem Festkörperblock eine volumetrische Wärmequelle hinzugefügt wird, wird die gesamte Wärmeerzeugung für den gesamten Festkörperblock (wie in Abbildung 2 gezeigt) auf einen einzelnen Volumenknoten angewendet. In diesem Fall sind bei Verwendung der thermischen Netzwerkmethode die Temperaturen deutlich höher als der theoretische Wert (die analytische Lösung, die aus der eindimensionalen Wärmeleitungsgleichung erhalten wird), wie in Abbildung 3 gezeigt.

Bei der Simulation von Fällen mit volumetrischen Wärmequellen neigt die thermische Netzwerkmethode dazu, Knotentemperaturen zu überschätzen. Daher ist eine spezielle Behandlung für thermische Netzwerksimulationen mit volumetrischen Wärmequellen erforderlich, um Genauigkeit zu gewährleisten, und dies wird in Teil zwei behandelt.

Die LPTN-Methode ist ein universeller Ansatz, der nicht nur auf Temperaturfeldberechnungen anwendbar ist, sondern auch auf Fluidströmung, elektrische Felder, magnetische Felder und mehr.

Referenzen:

[1] K&K Associates. Thermal Network Modeling Handbook[M]. K&K Associates, 2000.

[2] Dieter Gerling, Gurakuq Dajaku. Novel lumped-parameter thermal model for electrical systems[J]. DAJAKU Gurakuq, 2005.