Verbesserung der Genauigkeit bei der Lumped-Parameter Thermal Network (LPTN) Methode

Im vorherigen Artikel haben wir die grundlegenden Prinzipien der Lumped-Parameter Thermal Network (LPTN) Methode eingeführt und gezeigt, wie sie zur Modellierung der Wärmeübertragung mithilfe äquivalenter thermischer Widerstände verwendet werden kann. Das eindimensionale Wärmeübertragungsbeispiel veranschaulichte, wie die LPTN-Methode Temperaturverteilungen in Systemen ohne interne Wärmequellen genau vorhersagen kann. Wenn jedoch volumetrische Wärmeerzeugung eingeführt wird, neigt die LPTN-Methode dazu, die Temperatur zu überschätzen.

Da der LPTN-Ansatz weithin zur Simulation der Motortemperatur eingesetzt wird, wobei verschiedene Motorverluste als interne Wärmequellen modelliert werden, ist die Verbesserung seiner Genauigkeit für solche Probleme von entscheidender Bedeutung. Dieser Artikel untersucht mehrere Methoden zur Verbesserung des LPTN-Modells, wenn volumetrische Wärmequellen beteiligt sind.

1. Forschungsfall

Die Studie verwendet denselben massiven Block, der im ersten Artikel als Forschungsbeispiel eingeführt wurde.

Abbildung 1: Abmessungen des Festkörperblocks

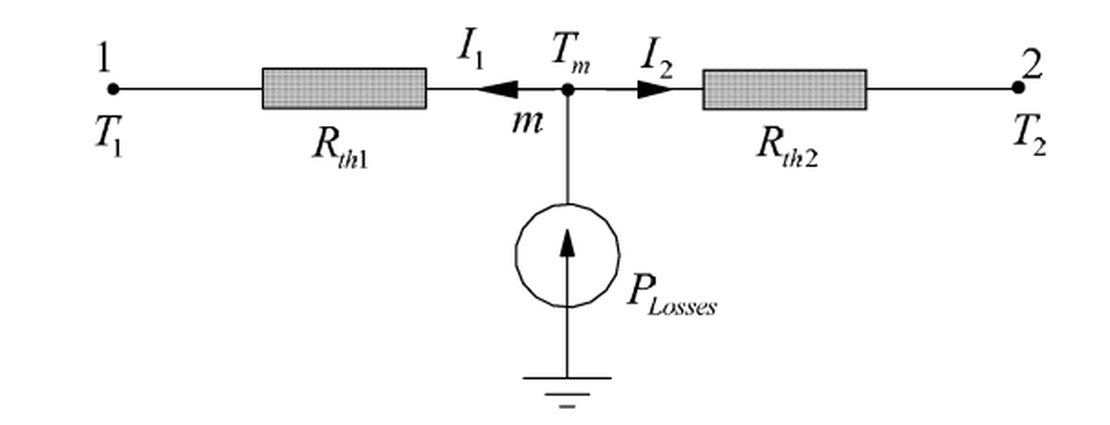
Abbildung 2: Thermisches Netzwerkdiagramm des Festkörperblocks

Ein massiver rechteckiger Block wird an seinen beiden Enden bei konstanten Temperaturen $T_1$ und $T_2$ gehalten, während er einer gleichmäßigen volumetrischen Wärmequelle ausgesetzt ist. Die Wärmeübertragung erfolgt entlang der x-Richtung des Blocks. Die geometrische Konfiguration und die entsprechende thermische Netzwerkdarstellung mit drei Knoten sind in den Abbildungen 1 und 2 dargestellt.

1.1 LPTN-Methode

Gemäß der LPTN-Methode können die Temperaturbeziehungen und Wärmeströme aus den ERhaltungsgleichungen abgeleitet werden, die in Teil 1 beschrieben sind.

\sum_{j=1}^{n} \dot{Q}_{ij} + S_i = \rho_i V_i C_{pi} \frac{dT_i}{dt} \tag{1}

Durch Einsetzen der thermischen Widerstände und Wärmeerzeugungsterme erhalten wir die Temperaturverteilung innerhalb des vereinfachten thermischen Netzwerks.

1.2 Analytische Lösung

Die analytische Lösung für dasselbe Problem kann aus der eindimensionalen stationären Wärmeleitungsgleichung mit einer volumetrischen Wärmequelle erhalten werden:

\frac{d^2 T}{dx^2} + \frac{\dot{q}}{k} = 0 \tag{2}

Randbedingungen:

T(0) = T_1, \quad T(L) = T_2 \tag{3}

Zweimaliges Integrieren ergibt:

T(x) = -\frac{\dot{q}}{2k}x^2 + C_1x + C_2 \tag{4}

Die Konstanten $C_1$ und $C_2$ werden mithilfe der Randbedingungen bestimmt.

1.3 Vergleich der Ergebnisse

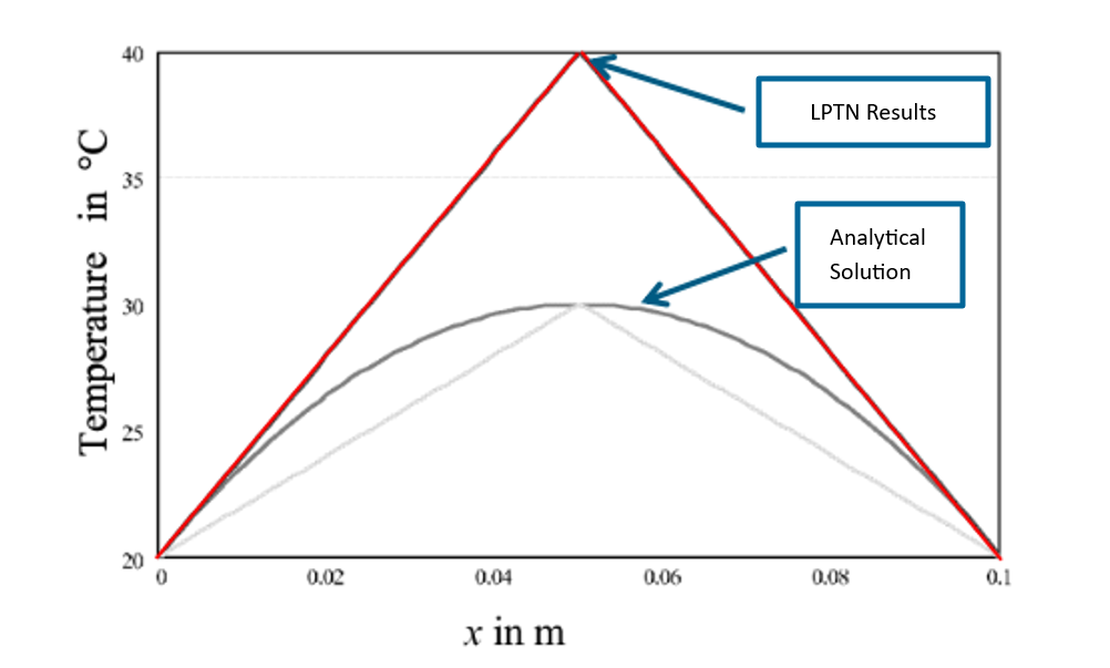
Abbildung 3: Vergleich zwischen LPTN und analytischen Ergebnissen

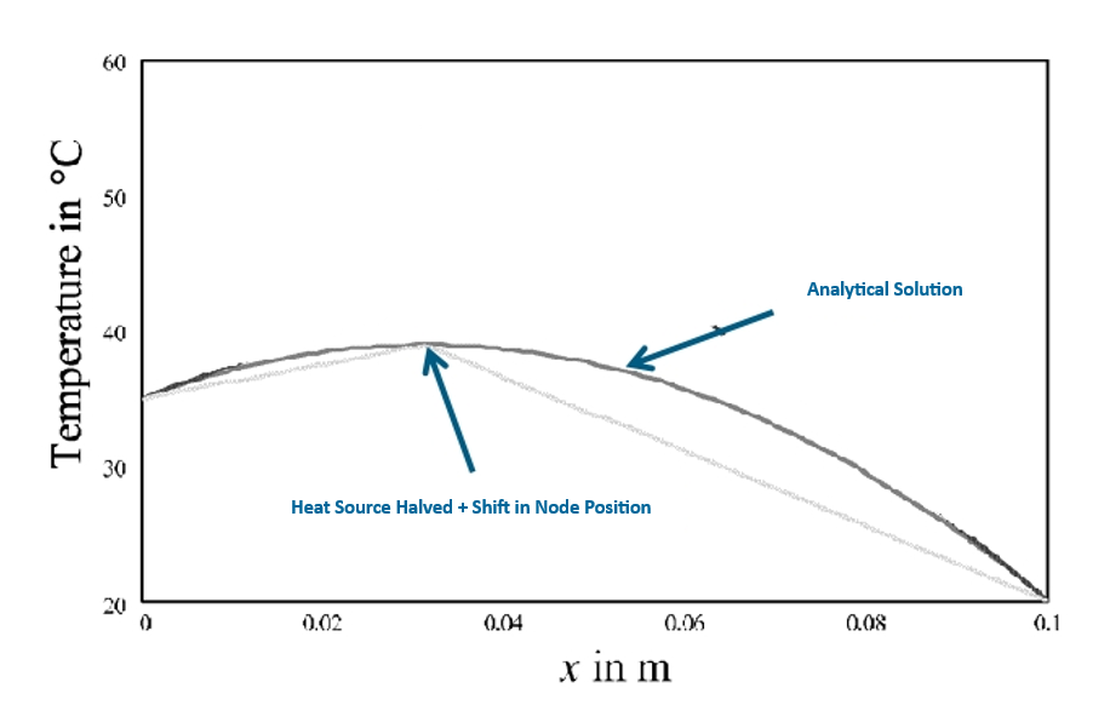
Wie in Abbildung 3 dargestellt, ist die durch die Lumped-Parameter Thermal Network (LPTN)-Methode vorhergesagte Temperatur deutlich höher als die aus der analytischen Lösung erhaltene.

Diese Diskrepanz tritt auf, weil die volumetrische Wärmequelle im gesamten Festkörper verteilt ist, während die LPTN-Methode die gesamte Wärmequelle an einem einzigen Netzwerkknoten konzentriert, sie also im Wesentlichen als Punktquelle behandelt. Infolgedessen wird die Mittelpunkttemperatur künstlich erhöht, was zu einer Überschätzung im Vergleich zum analytischen Ergebnis führt.

2. Korrekturmethoden

Um die Überschätzung der Temperatur in Fällen mit volumetrischen oder streifenförmigen Wärmequellen zu beheben, werden drei Verbesserungsmethoden vorgeschlagen:

Korrektur der Wärmequellen
Hinzufügen zusätzlicher thermischer Widerstände
Erhöhung der Knotenanzahl

2.1 Korrektur der Wärmequellen

Die Hauptursache für die Überschätzung ist die Vernachlässigung der räumlichen Verteilung der volumetrischen Wärmequelle. Wenn die Gesamtwärme innerhalb des Netzwerks genauer dargestellt wird, kann die Temperaturvorhersage verbessert werden.

Untersuchungen zeigen, dass der analytische Wärmestrom zwar über den gesamten Bereich variiert, seine Änderungsrate jedoch konstant bleibt. Daher führt die Anpassung der angewendeten Wärmequelle im LPTN-Modell, wie beispielsweise die Reduzierung auf die Hälfte der ursprünglichen Größenordnung, dazu, dass die Ergebnisse mit der analytischen Lösung übereinstimmen.

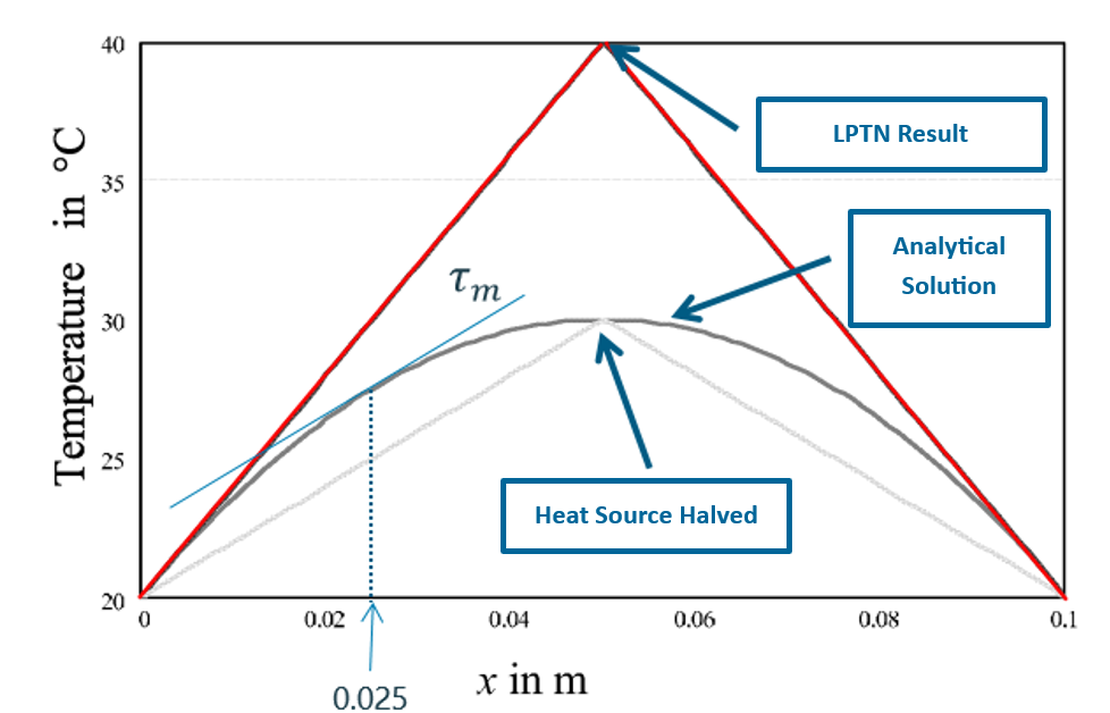
Abbildung 4: Vergleich der Temperaturergebnisse zwischen der Wärmequellen-Halbierungsmethode und der analytischen Lösung unter Verwendung der LPTN-Methode

Wenn beide Randtemperaturen gleich sind, entspricht der Mittelpunkt dem Ort der maximalen Temperatur.
Wenn sich die Randtemperaturen jedoch unterscheiden, verschiebt sich der Punkt der maximalen Temperatur in Richtung der heißeren Grenze. Seine Position kann aus der analytischen Lösung abgeleitet werden:

x_{\text{max}} = \frac{L(T_1 - T_2)}{\dot{q}L^2 / (2k) + (T_1 - T_2)} \tag{5}

Um die korrekte Maximaltemperatur zu bestimmen, kann die Knotenposition innerhalb des thermischen Netzwerks iterativ auf Basis der Randtemperaturen angepasst werden, bis Konvergenz erreicht ist.

Abbildung 5: Vergleich der Temperaturergebnisse zwischen der Wärmequellen-Halbierungsmethode + Knotenpositionsverschiebung und der analytischen Lösung

2.2 Zusätzlicher thermischer Widerstand

Die grundlegende Gleichung für Wärmeleitung mit interner Wärmeerzeugung ist die Poisson-Gleichung. Aufgrund ihrer Linearität kann es mithilfe des Superpositionsprinzips in zwei unabhängige Probleme zerlegt werden:

Ein Problem, das reine Wärmeleitung (ohne Wärmequelle) darstellt.
Ein Problem, das den Temperaturanstieg aufgrund der Wärmequelle darstellt.

Das Teilproblem ohne Wärmequellen stimmt gut mit der LPTN-Annahme überein. Das zweite Teilproblem, das die Wärmeerzeugung darstellt, kann als zusätzlicher korrigierender thermischer Widerstand im Netzwerk modelliert werden.

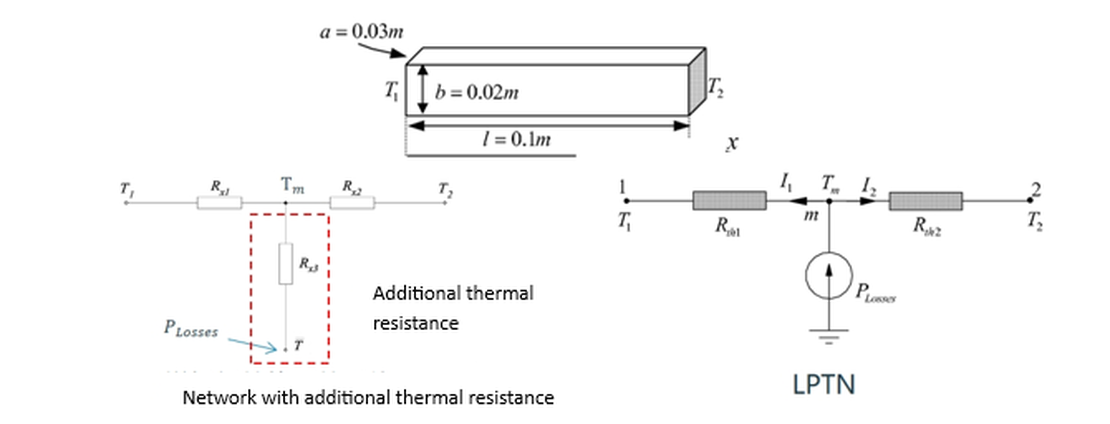
Abbildung 6: Temperaturkorrigiertes thermisches Netzwerkdiagramm

Für dieses modifizierte Netzwerk kann der zusätzliche Korrekturwiderstand $R_{x3}$ wie folgt abgeleitet werden:

\frac{d^2 T}{dx^2} = -\frac{\dot{q}}{k} \tag{6}

Mit Randbedingungen:

T(0) = 0, \quad T(L) = 0 \tag{7}

Integration ergibt die mittlere Korrekturtemperatur $\bar{T}$ :

\bar{T} = \frac{\dot{q}L^2}{12k} \tag{8}

Der äquivalente Korrekturwiderstand kann aus Energiebilanzbetrachtungen ermittelt werden:

R_{x3} = -\frac{L}{6kA} \tag{9}

Der negative Wert von $R_{x3}$ impliziert einen scheinbaren Wärmefluss von einer niedrigeren zu einer höheren Temperaturregion, physikalisch unrealistisch aber rechnerisch effektiv. Es gleicht die Temperaturüberschätzung des LPTN aus, indem es die vorhergesagte Mittelpunkttemperatur senkt.

Wenn $\dot{q} = 0$ , reduziert sich die Gleichung auf das traditionelle LPTN-Modell ohne interne Quellen.

2.3 Erhöhung der Netzwerkknoten

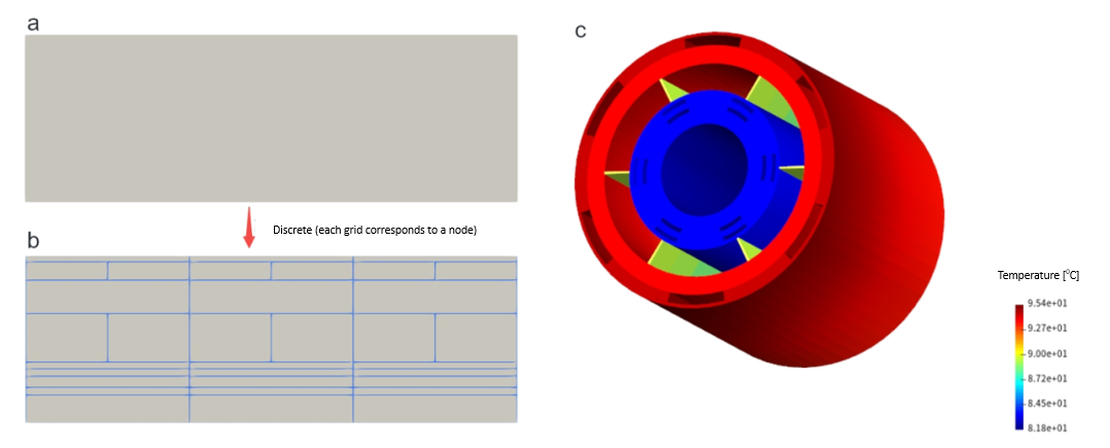
Da traditionelle LPTN-Modelle die gesamte Geometrie in wenigen Knoten zusammenfassen, verlieren sie räumliche Auflösung und sind weniger genau für Systeme mit verteilter Wärmeerzeugung. Die Erhöhung der Anzahl der Knoten hilft dabei, diese räumliche Abhängigkeit effektiver zu erfassen.

Im Grenzfall einer unendlichen Anzahl von Knoten kann die analytische Temperaturverteilung exakt reproduziert werden. Dieser Ansatz erhöht jedoch den Rechenaufwand und die Modellierungskomplexität.

Moderne Werkzeuge wie shonTA verwenden flexible Vorlagen, die eine beliebige Knotendiskretisierung sowohl in axialer als auch in radialer Richtung ermöglichen. Mit Unterstützung der parallelen Berechnung können diese Modelle Genauigkeit und Effizienz ausbalancieren.

shonTA-Motorvorlage zeigt a) Umfangsprojektion des Rotors; b) Diagramm der diskreten Knoten; c) Konturdiagramm des Temperaturfelds — Abbildung 7: shonTA-Motorvorlage zeigt a) die geometrische Umfangsprojektion des Rotors; b) das Diagramm der diskreten Knoten des Rotors; c) das Konturdiagramm des Temperaturfelds des Rotors

3. Zusammenfassung

Wenn volumetrische Wärmequellen vorhanden sind, neigen konventionelle thermische Netzwerkmethoden dazu, Temperaturen im Vergleich zu analytischen Ergebnissen zu hoch vorherzusagen.
Drei praktische Korrekturstrategien stehen zur Verfügung:

Korrekturmethode für Wärmequellen
- Passt die Gesamtwärmeerzeugung an (z. B. Halbierung der Wärmequelle).
- Entspricht der maximalen Temperatur, reduziert aber die Gesamtsystemenergie.
- Erfordert eine Knotenverschiebung, wenn sich die Randtemperaturen unterscheiden.
Zusätzlicher thermischer Widerstand-Methode
- Führt einen korrigierenden negativen Widerstand ein, um die Überschätzung auszugleichen.
- Gewährleistet eine genauere durchschnittliche Temperatur.
Erhöhung der Netzwerkknoten
- Verbessert die räumliche Genauigkeit.
- Erhöht den Rechenaufwand und den Modellierungsaufwand.

Diese Techniken verbessern gemeinsam die Zuverlässigkeit der LPTN-Methode für Systeme mit interner Wärmeerzeugung, wie elektrische Maschinen und Wärmesysteme mit hoher Dichte.

Referenzen

[1] Dieter Gerling, Gurakuq Dajaku. Novel lumped-parameter thermal model for electrical systems. 2005.
[2] R. Wrobel, P. H. Mellor. A General Cuboidal Element for Three-Dimensional Thermal Modelling. IEEE Transactions on Magnetics, 2010.

Kontakt aufnehmen

Fordern Sie eine kostenlose Testversion an oder kontaktieren Sie uns direkt

Verbesserung der Genauigkeit bei der Lumped-Parameter Thermal Network (LPTN) Methode (2/2)