Die Schmierung von Getrieben ist ein kritischer Aspekt der Aufrechterhaltung effizienter und langlebiger Getriebesysteme. Es beinhaltet das Auftragen von Schmierstoffen, um Reibung zu verringern, Wärme abzuleiten und Verschleiß sowie Korrosion in Getriebesystemen zu verhindern. Eine ordnungsgemäße Getriebeschmierung gewährleistet einen reibungslosen Betrieb, verlängert die Lebensdauer der Komponenten und trägt zur Gesamtzuverlässigkeit des Systems bei.
Fallbeschreibung
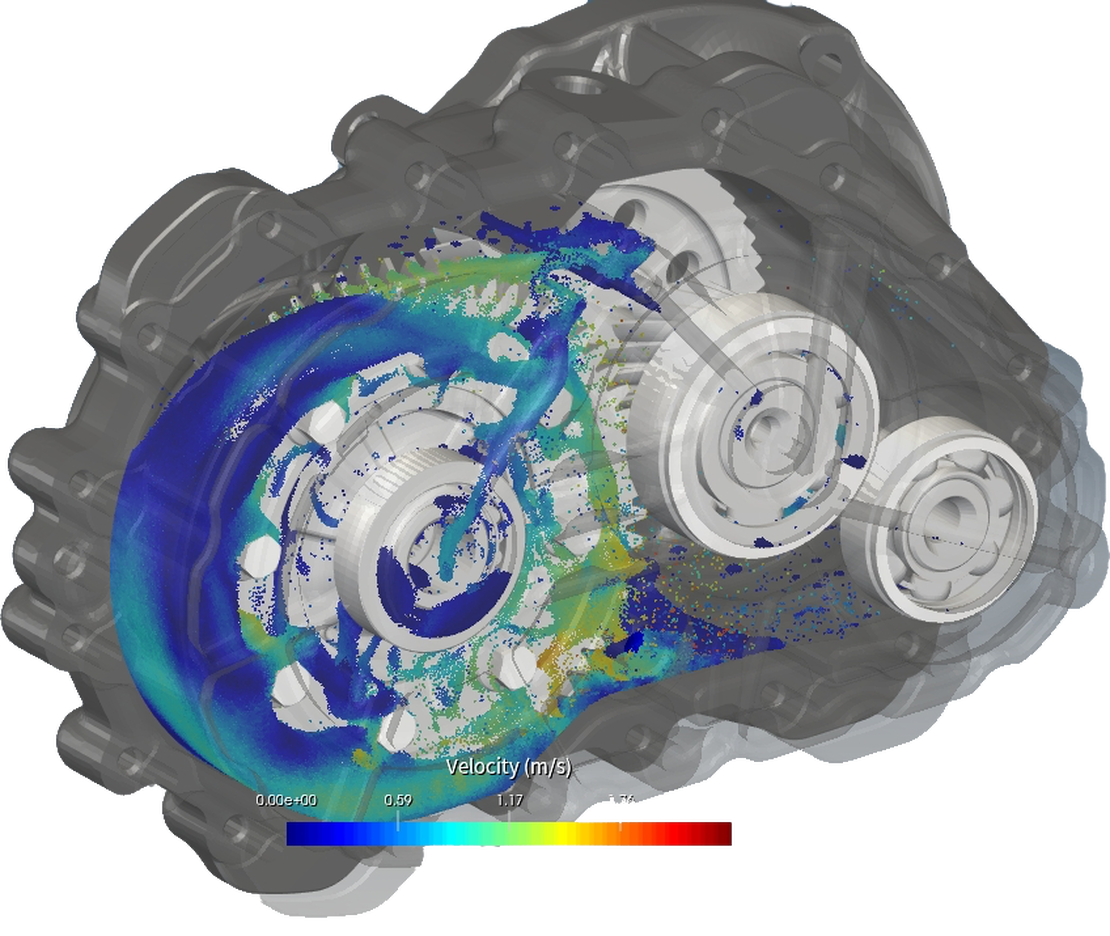
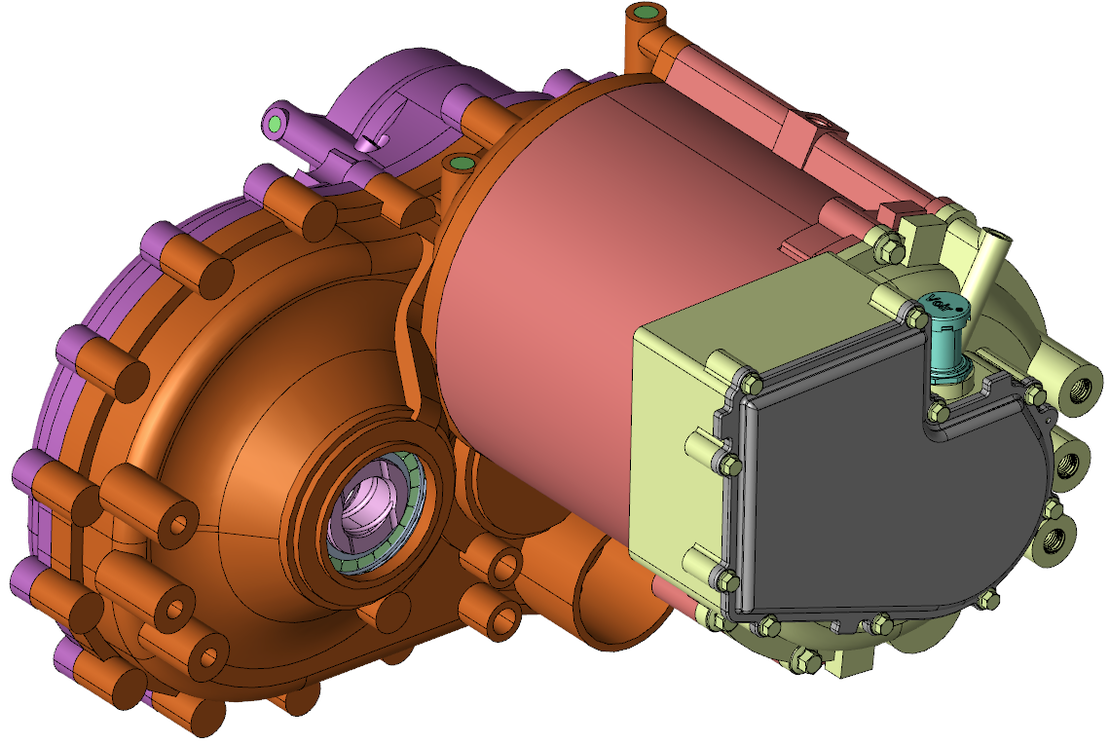
In diesem Fall war das Ziel, Simulationsergebnisse mit experimentellen Befunden zu vergleichen. Hinsichtlich der Schmierung sind die markierten Bereiche in den folgenden Abbildungen entscheidend. Der rote Kreis hebt die Lager hervor, und die Pfeile zeigen auf kleine Kanäle, die zu diesen Kammern vor den Lagern führen. In der Simulation werden diese Regionen mit Stichprobenfenstern überwacht, um eine quantitative Vorstellung von der Menge der Flüssigkeit in den Lagern und dem Fluss zu den Kammern zu erhalten. Auf dem Bild des Experiments sind die gleichen Bereiche grün hervorgehoben. Um die Lager effizient zu schmieren, müssen die Kammern durch die Kanäle mit Schmierstoff gefüllt werden. Durch den Vergleich dieser kritischen Bereiche bei verschiedenen Drehgeschwindigkeiten mit den experimentellen Ergebnissen kann ermittelt werden, wie genau die Simulationen sind.


Simulations Setup
Für die Simulation wurde die gleiche Menge an Schmiermittel verwendet wie im Experiment, d.h. 300 ml. Es wurde ein Partikelradius von 0,42 mm gewählt, was zu einer Partikelanzahl von ungefähr einer halben Million Partikeln führte. Die Eigenschaften der Flüssigkeit sind in der untenstehenden Tabelle aufgeführt. Mit diesen Eigenschaften stellt die Flüssigkeit ein Schmiermittel bei 20°C dar.
| Parameter | Wert |
|---|---|
| Dichte der Flüssigkeit | 884 kg/m3 |
| Kinematische Viskosität | 0,16E-4 m2/s |
| Oberflächenspannung | 0,021 N/m |
| Schwerkraft | 9,81 m/s2 |
Das hier verwendete Getriebe verfügt über Stirnräder. Innerhalb dieses Getriebes gibt es zwei Zahnräder mit unterschiedlichen Übersetzungsverhältnissen. Das erste Zahnradpaar hat ein Verhältnis von 0,4468. Das zweite Paar hat ein Verhältnis von 0,3607. Werden diese Verhältnisse kombiniert, ergibt sich ein Gesamtübersetzungsverhältnis von 0, 1611, was zu einer Drehgeschwindigkeit von 0, 1611 Umdrehungen pro Minute (RPM) an der Ausgangswelle für jede Umdrehung an der Eingangswelle führt - eine erhebliche Verringerung der Geschwindigkeit vom Eingang zum Ausgang des Getriebes,
Untersuchte Fälle:
| Fall | Eingangsdrehzahl (U/min) | Ausgangsdrehzahl (U/min) |
|---|---|---|
| Fall 1 | 480 | 77,34 |
| Fall 2 | 980 | 157,9 |
| Fall 3 | 1453 | 234,1 |
Ergebnisse
Fall 1: 480 U/min
In den unten bereitgestellten Videos beobachten wir Fall 1, bei dem die Eingangsdrehzahl auf 480 U/min eingestellt ist.
Bei der Analyse der Simulationsergebnisse wird deutlich, dass eine Ausgangsdrehzahl von 77 U/min nicht ausreicht, um das kleine Becken oben am Getriebe angemessen zu füllen. Das Becken ist mit einem roten Kreis im Video gekennzeichnet. Die dabei wirkenden Dynamiken zeigen auf, dass das große Zahnrad in die Flüssigkeit greift und sie etwa zu zwei Dritteln der Höhe des Zahnrads anhebt, nur um sie anschließend wieder in das Reservoir zurückfallen zu lassen.
Als Konsequenz können die Kanäle, die zur mittleren Kammer führen, bei dieser Geschwindigkeit nicht gefüllt werden. Zusätzlich bleibt der Kanal zur linken Kammer, welcher nicht mit dem Becken verbunden ist, auch leer.
Es kann daraus geschlossen werden, dass bei dieser Ausgangsgeschwindigkeit keine Schmierung der Lager stattfindet. Die Ausgangsgeschwindigkeit behindert einen ordnungsgemäßen Fluss der Flüssigkeit zu den wesentlichen Komponenten.
Vergleichend zu diesen Beobachtungen der Simulation mit dem Video des Experiments, lässt sich feststellen, dass die Simulation gut mit den experimentellen Ergebnissen übereinstimmt.
Fall 2: 980 U/min
In den untenstehenden Videos wird Fall 2 mit einer Eingangsdrehzahl von 980 U/min dargestellt.
Laut den Simulationsergebnissen erweist sich eine Ausgangsgeschwindigkeit von 158 U/min als ausreichend, um das kleine Becken oben zu füllen. Folglich sind die Kanäle, die zur mittleren Kammer führen, ausreichend mit Flüssigkeit gefüllt. Zusätzlich ist auch der Kanal zur linken Kammer gefüllt. Es ist zu beobachten, dass sowohl das Becken als auch die linke Kammer nicht mit einem kontinuierlichen Schmierstofffluss gefüllt werden, sondern mit einem oszillierenden Fluss.
Das erfolgreiche Füllen des Beckens und der linken Kammer bei der angegebenen Ausgangsgeschwindigkeit deutet auf eine verbesserte Leistung im Vergleich zu Fall 1 hin, was die Bedeutung der Eingabegeschwindigkeit für eine angemessene Schmierung und Flüssigkeitsverteilung der mittleren und der linken Kammer Beispielhaft aufzeigt. Leider wird die rechte Kammer nicht durch den Kanal befüllt, der die Mitte und die linke Kammer verbindet.
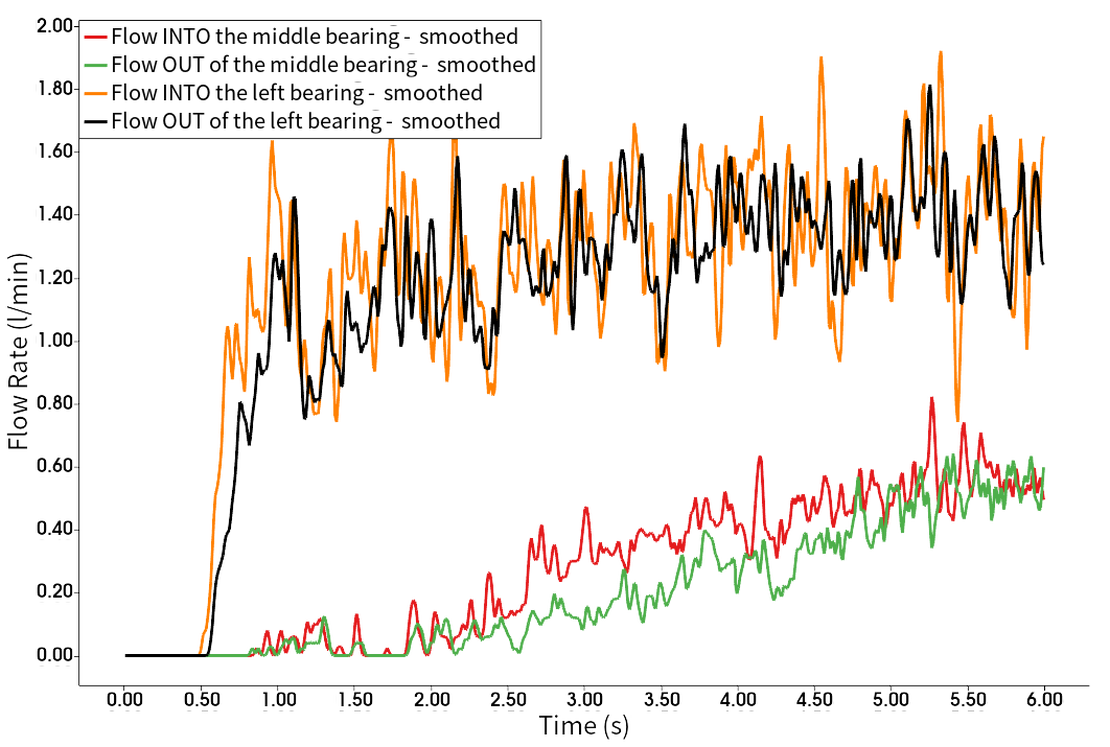
Um die Simulationsergebnisse mit den experimentellen Ergebnissen zu vergleichen, ist es unerlässlich, einen quasi-stationären Zustand zu erreichen. Ein Indikator für diesen Zustand ist das Gleichgewicht der Probenfenster, was bedeutet, dass im Durchschnitt der Flüssigkeitsfluss in die und aus den Probenfenstern beinahe gleich ist. Das Diagramm unten veranschaulicht dieses Verhalten.
Im linken Lager wird ein stationärer Zustand bereits nach etwa 2 Sekunden erreicht, während es beim mittleren Lager deutlich länger dauert. Nach 5 Sekunden kann davon ausgegangen werden, dass der stationäre Zustand im Mittellager erreicht ist. Diese Analyse betont die Wichtigkeit, dem System ausreichend Zeit zu geben, um sich zu stabilisieren, bevor aussagekräftige Vergleiche zwischen Simulation und experimentellen Ergebnissen gezogen werden.
Beim Vergleichen dieser Beobachtungen aus der Simulation mit dem Video des Experiments lässt sich visuell feststellen, dass die linke Kammer gut mit den experimentellen Befunden übereinstimmt. Allerdings ist ein leicht überprognostizierendes Verhalten am oberen Ende des Getriebes erkennbar. Die Simulation suggeriert eine nicht zu vernachlässigende Füllung des Beckens, aber bei genauerer Betrachtung des zweiten Teils des Videos des Experiments (ab 6 Sekunden) wird deutlich, dass die Flüssigkeit zwar die Unterseite des Beckens zu berühren scheint, aber der größte Teil der Flüssigkeit nicht in das Becken gelangt. Folglich scheint der Kanal zur mittleren Kammer weniger Flüssigkeit zu transportieren als in der Simulation.
Fall 3: 1453 U/min
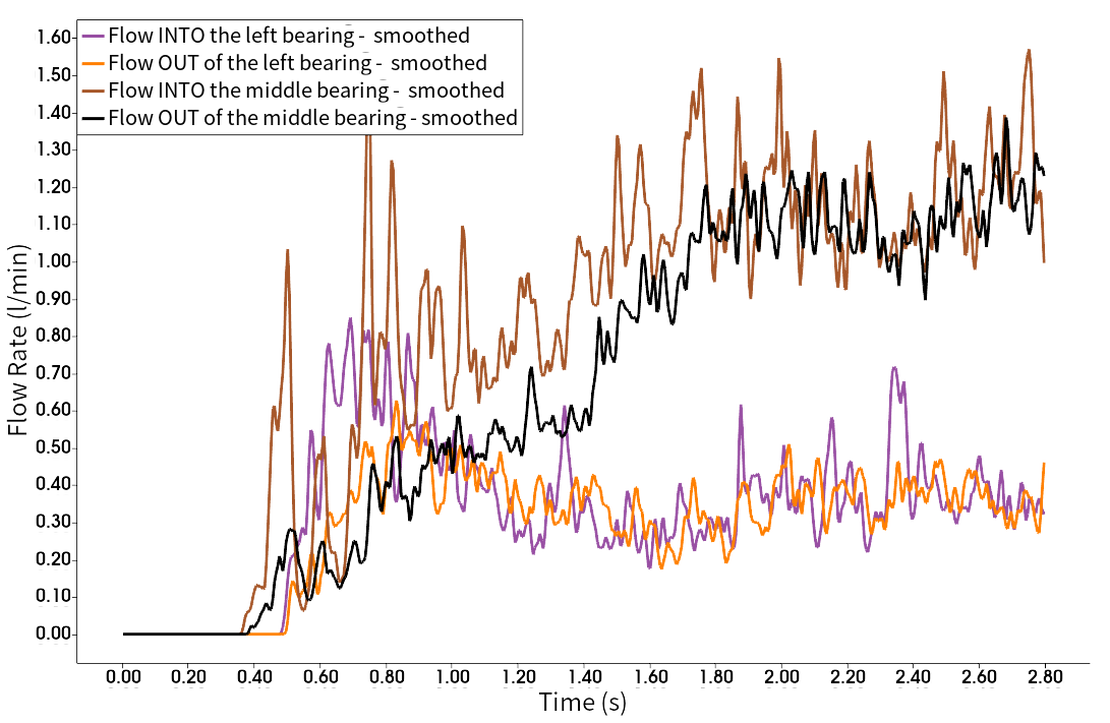
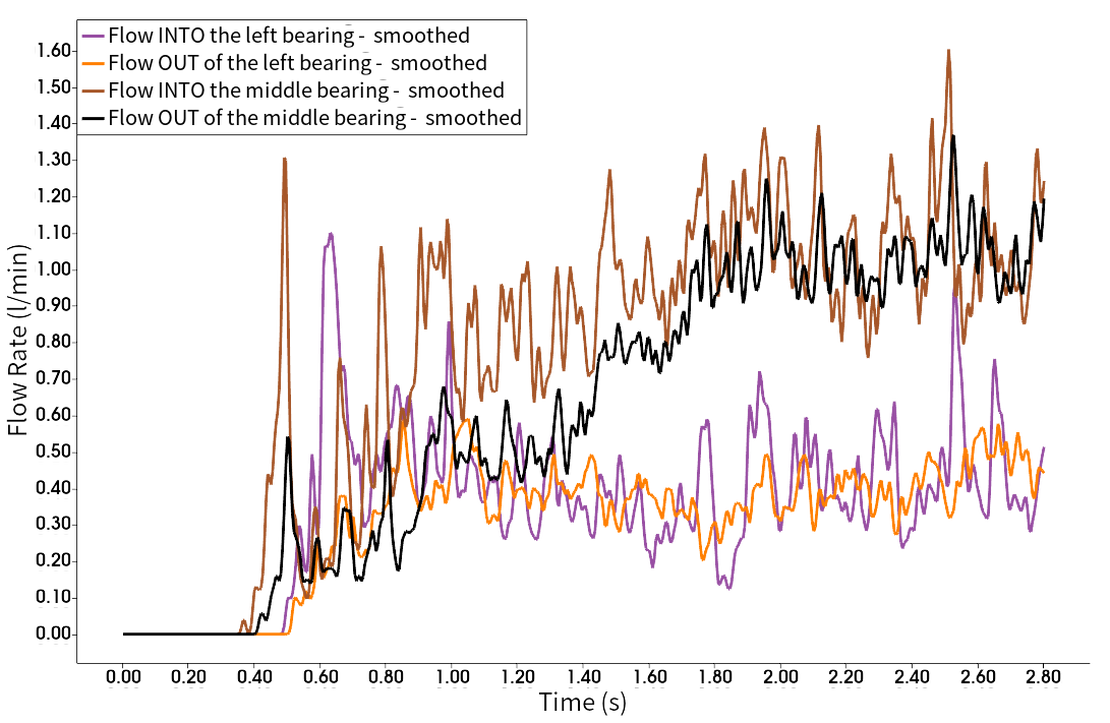
Auch wenn Fall 3 eine höhere Eingangsgeschwindigkeit als Fall 2 aufweist, zeigt der Schmierprozess nahezu dieselbe Gesamtleistung. Ähnlich wie bei Fall 2 sind die Kammern der linken und mittleren Lager ausreichend gefüllt, während das rechte Lager und die Kammer minimal bis gar nicht geschmiert werden. Der Hauptunterschied zu Fall 2 liegt darin, dass der stationäre Zustand in Fall 3 viel früher erreicht wird. Dies kann in der unten stehenden Grafik beobachtet werden, die die Zu- und Abläufe der Probe-Fenster der linken und mittleren Lager illustriert.
In beiden Lagern wird ein Gleichgewicht erreicht, was darauf hinweist, dass die gleiche Menge an Flüssigkeit in das Probenfenster einfließt, wie sie herausfließt. Laut dem Diagramm wird der stationäre Zustand bereits nach 1,8 Sekunden erreicht. Das frühe Erreichen eines Gleichgewichtszustandes deutet auf eine schnellere Stabilisierung des Schmierprozesses in Fall 3 im Vergleich zu Fall 2 hin. Allerdings bleibt das anhaltende Problem der unzureichenden Schmierung im rechten Lager und Kammer bestehen, was weitere Untersuchungen oder Änderungen erfordert, um diese spezielle Herausforderung zu bewältigen.
Beim Vergleichen dieser Beobachtungen aus der Simulation mit dem Video des Experiments lässt sich visuell feststellen, dass die linke Kammer die Füllung im Video des Experiments leicht unterschätzt. Andererseits sieht die Füllung des Pools in der Simulation und im Experiment vergleichbar aus. Folglich transportiert der Kanal zur Mittelkammer sowohl in der Simulation als auch im Experiment mehr Flüssigkeit als im Fall 2.
Schlussfolgerung
Im Fall 1 (480 U/min) stimmt die Simulation gut mit den experimentellen Ergebnissen überein und offenbart eine unzureichende Schmierung bei der angegebenen Ausgangsdrehzahl. Fall 2 (980 U/min) zeigt eine verbesserte Leistung der Schmierung, mit einer guten Übereinstimmung zwischen Simulation und Experiment. Im Fall 3 (1453 U/min) erfasst die Simulation frühe stationäre Zustände und konsistente Trends, wobei eine zufriedenstellende Übereinstimmung mit experimentellen Beobachtungen gezeigt wird, insbesondere beim Füllen des Beckens an der Spitze des Getriebes.
Studie zur Auflösung
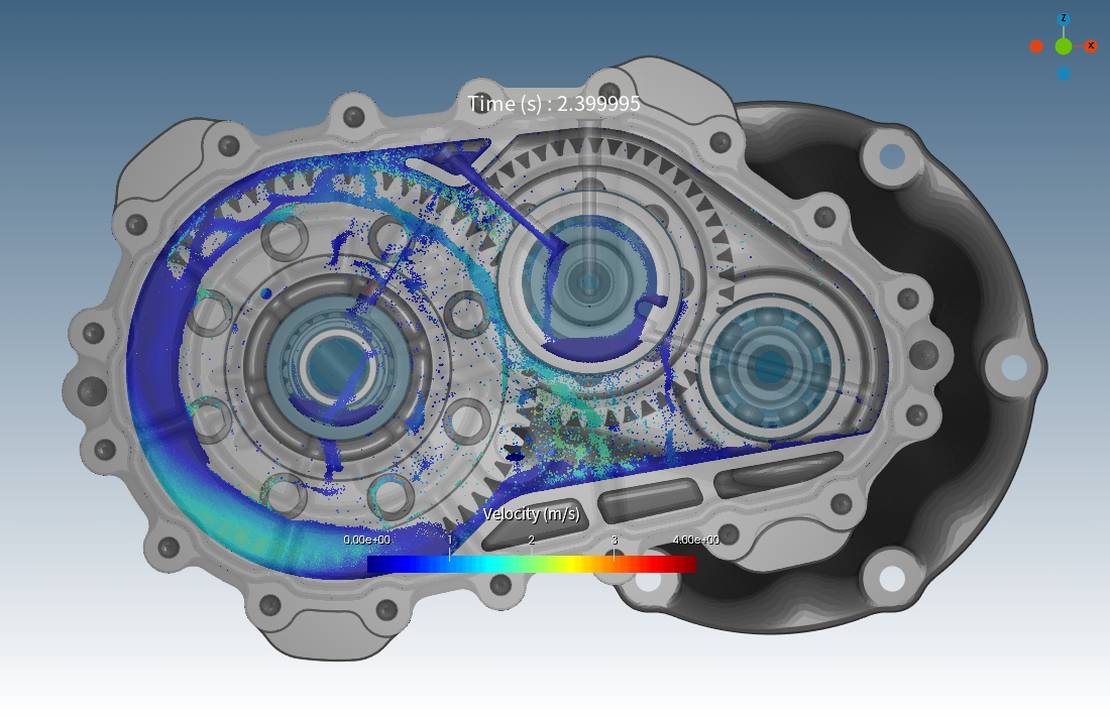
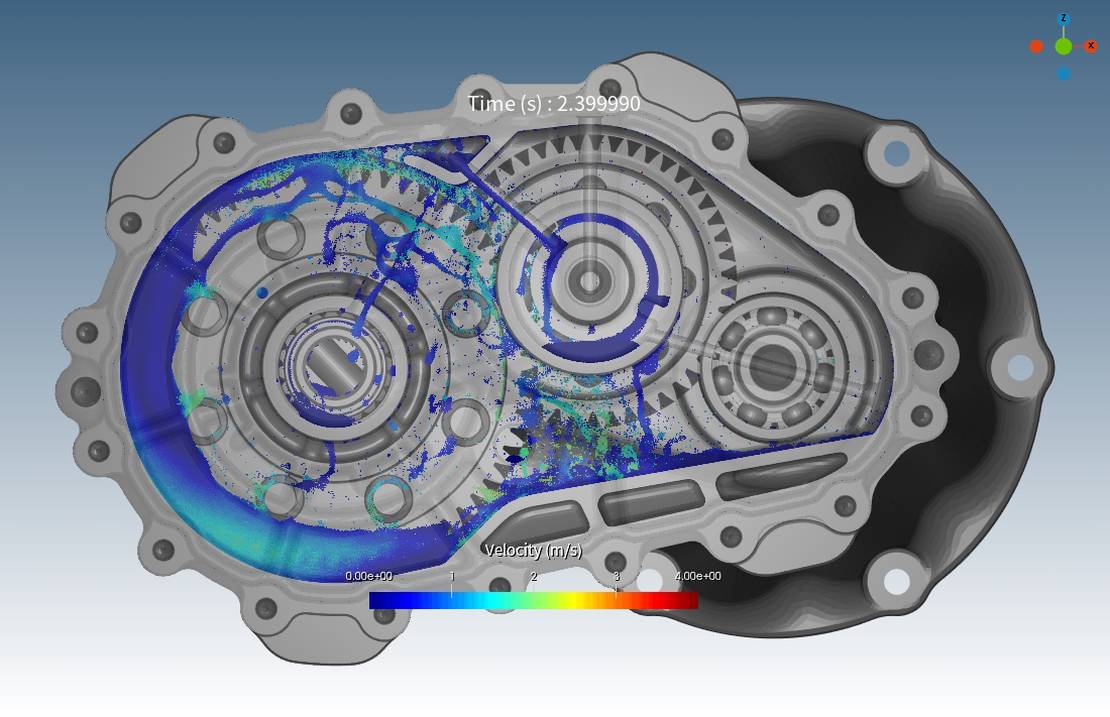
In traditionellen Finite-Volumen-Methoden (FVM) CFD-Simulationen ist eine Netzstudie üblich, während bei partikelbasierten Methoden das Gegenstück eine Untersuchung der Partikelgröße ist. In dieser Simulation wurde zunächst eine Studie zur Partikelgröße durchgeführt und hier am Ende teilweise präsentiert, wobei zwei Auflösungen gezeigt werden: der Basisfall (Fall 3) mit 0,5 Millionen Partikeln und der Fall mit höherer Auflösung (Fall 3 High Res) mit 1 Million Partikeln. Als Referenzwerte für die Zuström- und Abströmrate in und aus dem Lager wurden in beiden Fällen vergleichbares Verhalten festgestellt, wie in den untenstehenden Diagrammen gezeigt wird. Dies bestätigt, dass 0,5 Millionen Partikel für diese Szenarien ausreichend sind. Snapshots bei 2,4 Sekunden aus beiden Simulationen unterstützen dies weiterhin, indem sie eine ähnliche Flüssigkeitsverteilung und -verhalten anzeigen.

Zusammenfassung der Rechenstatistiken
| Komponente | Beschreibung |
|---|---|
| Betriebssystem | Windows |
| CPU | 12. Generation Intel(R) Core i9-12900K |
| RAM | 64 GB |
| GPU | NVIDIA GeForce RTX 3090 |
Die Simulationen wurden mit Version 2.6 durchgeführt.
Die Version 2.7 wird voraussichtlich deutlich schneller sein. Einen direkten Vergleich zwischen den Versionen 2.6 und 2.7 finden Sie hier: Gewässerdurchquerung
| Parameter | Fall 1 | Fall 2 | Fall 3 | Fall 3 High Res |
|---|---|---|---|---|
| Simulationszeit | 5,3 s | 6 s | 2,8 s | 2,8 s |
| Partikel Anzahl | 0,5 Millionen | 0,5 Millionen | 0,5 Millionen | 1 Million |
| Partikelradius | 0,42 mm | 0,42 mm | 0,42 mm | 0,33 mm |
| Rechenzeit | 5,3 h | 12,6 h | 8,1 h | 12,6 h |