In computational fluid dynamics (CFD), there’s more than one way to describe how fluids move, mix, and interact with their environment. For decades, the finite volume method (FVM) has served as the standard, forming the backbone of most commercial and academic CFD solvers. However, as applications become more complex, involving violent sloshing, free surfaces, or moving boundaries, particle-based CFD methods have emerged as a compelling alternative.
Both approaches solve the same governing physics, i.e., the Navier–Stokes equations. Yet, the way they represent fluids, compute interactions, and handle geometry is fundamentally different. Understanding these differences helps engineers choose the right numerical tool for the physics they want to capture.
From Grids to Particles – A Change in Perspective
The FVM approaches fluid motion from an Eulerian perspective. It divides the simulation domain into a grid of control volumes and calculates the flow of mass, momentum, and energy between them. In contrast, particle-based CFD takes a Lagrangian approach, focusing on the direct movement and interactions of discrete packets of fluid.
In FVM, the fluid moves through either a fixed or moving mesh, while in particle CFD, the mesh is absent, and a dynamic cloud of interacting particles represents the fluid. Although the difference may seem subtle, it has significant implications for numerical stability, flexibility, and scalability.
The Finite Volume Method
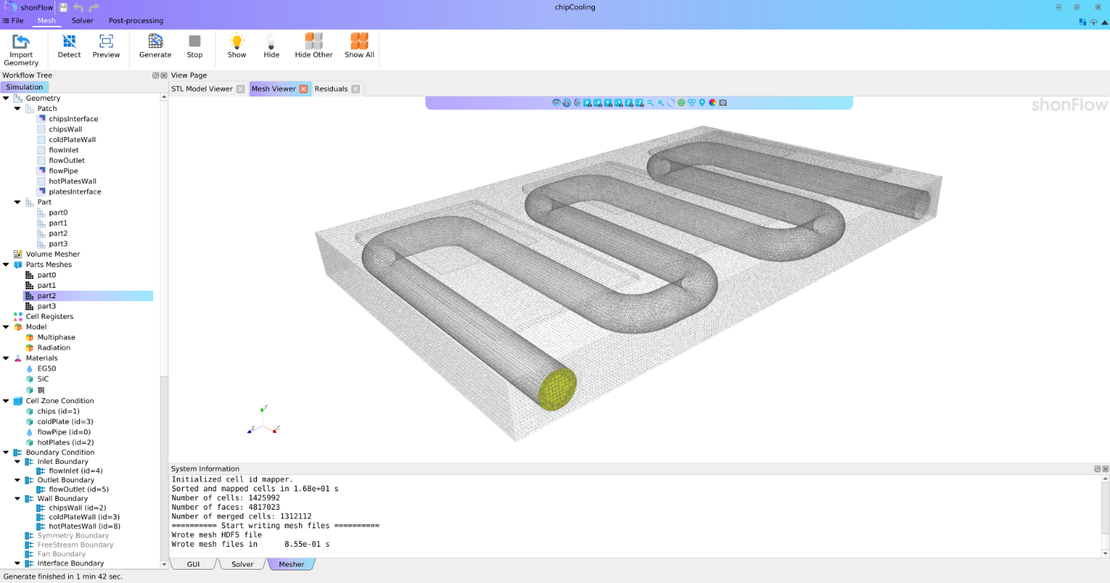
FVM is a fundamental technique in CFD because it upholds the principles of mass, momentum, and energy conservation. It ensures that the amount of matter entering one control volume equals the amount leaving the control volume. By integrating the conservation equations over each cell and utilizing the divergence theorem, FVM transforms differential equations into algebraic forms that solvers can efficiently handle. This framework guarantees global conservation, even when dealing with complex, unstructured meshes.
The advantages of FVM are well recognized:
- High numerical accuracy and strict conservation of fluxes.
- A wide range of turbulence and combustion models validated over decades.
- Robust handling of boundary conditions for walls, inlets, and outlets.
- Strong scalability on parallel computing architectures.
These features make FVM particularly suitable for applications where domain geometry is fixed and flow remains continuous, such as in aerodynamics, turbomachinery, or electronics cooling. However, FVM’s reliance on mesh quality presents challenges. When geometries deform or interfaces break apart, as in cases of splashing, fragmentation, or free-surface flows, maintaining mesh quality becomes increasingly complex.
The Particle-Based Approach
Particle CFD, on the other hand, abandons the mesh altogether. Each particle represents a small mass of fluid, carrying its own velocity, pressure, and thermodynamic properties. These particles interact through kernel functions that define their local neighbourhood.
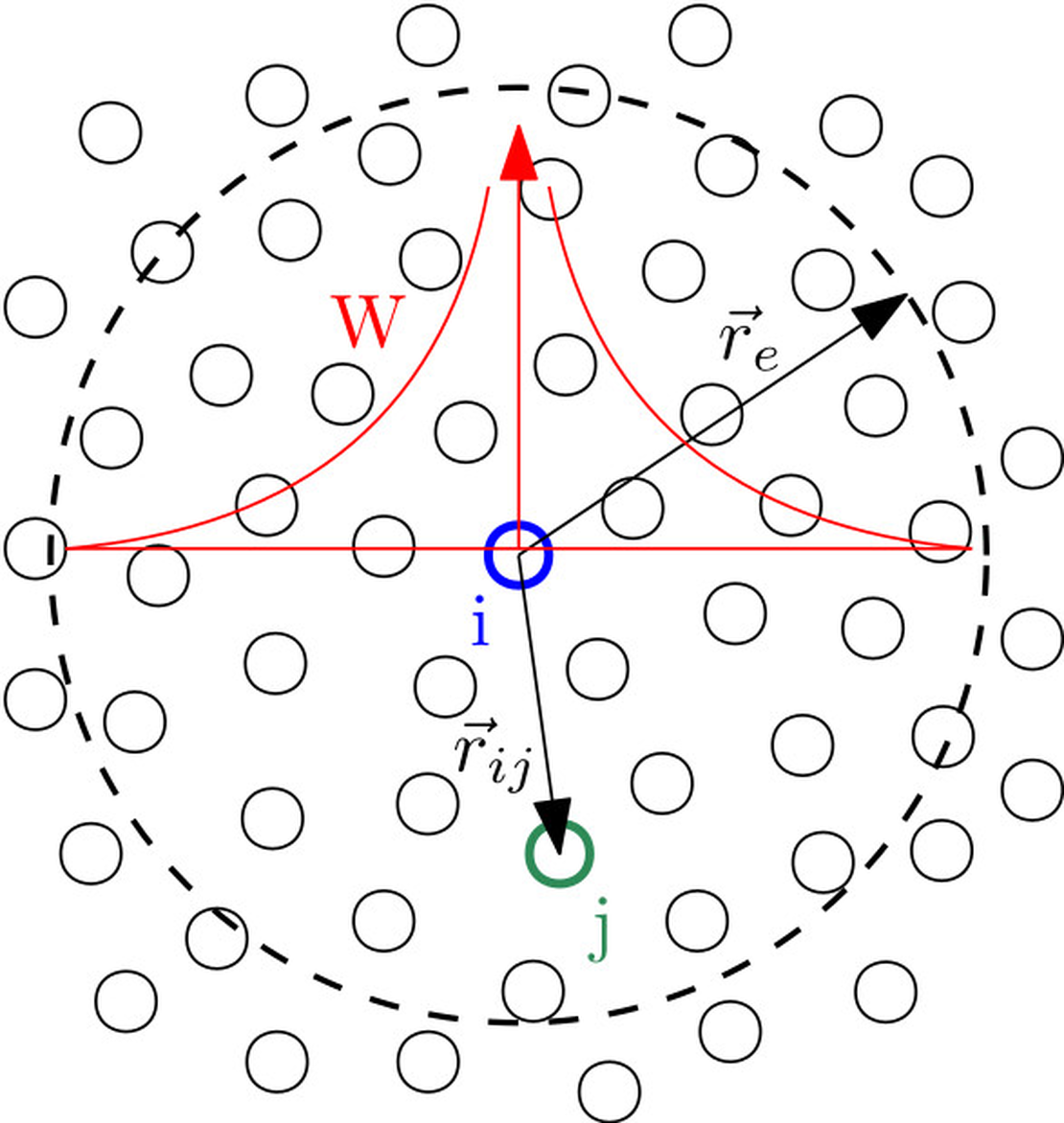
The importance of the influence of one neighboring particle to another can be calculated here through a simple weight function:
Popular variants of lagrangian based particle CFD are the Smoothed Particle Hydrodynamics Method (SPH) or Moving Particle Semi Implicit Method (MPS). Since the method is fully Lagrangian, the motion of particles naturally follows the flow. There’s no grid to deform, no need for remeshing, and no topological constraints.

This makes Particle CFD particularly powerful for:
- Free-surface and sloshing flows (e.g., liquid fuel tanks, wave–structure interactions).
- Fluid–structure interaction (FSI) where solid boundaries move or deform.
- Multiphase and granular systems, such as suspensions or powder flows.
- Phase-change processes, like melting, solidification, or spray dynamics.
Its mesh-free nature makes pre-processing far simpler, the geometry setup becomes faster, especially for complex or evolving domains.
Choosing the Right Approach
The choice between particle CFD and finite volume CFD is determined more by the physics of the problem than by personal preference:
- For steady-state, high-Reynolds-number, or thermal flows, the FVM is unparalleled.
- For highly transient, multiphase, or deforming systems, particle CFD effectively captures complexities that traditional meshes cannot.
Experienced simulation engineers increasingly view these two methods as complementary; they are like different instruments in the same numerical orchestra, each suited to a unique aspect of fluid motion.
Advancing CFD Beyond Traditional Boundaries
We currently see both particle CFD and FVM adopting to new compute architectures. This enables even larger and more detailed simulations for both approaches. Advances in moving and adaptable meshes in the field of FVM and variable particle sizes in Lagrangian CFD are pushing the boundaries of what’s possible even further and somehow show a convergence of the methods in their application fields on the horizon.
Ultimately, both finite volume and particle methods aim to help engineers visualize the unseen, specifically to predict the behaviour of fluids that shape our environment.

